Utilisateur:Jean-Michel Tanguy/SujetENTPE2021/JUILLARD - MESSIAEN - SARRADE

Contexte

En raison du changement climatique, le niveau des mers et des océans ne cesse d’augmenter. Cette hausse provoque de nombreuses conséquences sur le territoire et les habitants. En effet, l’érosion des côtes augmentent, détruisant les infrastructures et entraînant le départ des habitants.

A travers ce projet, nous étudierons l'impact du réchauffement climatique sur le littoral et notamment l’impact de la houle sur le littoral. Nous utiliserons le modèle de Berkhoff afin de modéliser les houles.

Le modèle de Berkhoff

Nous utilisons le modèle de Berkhoff afin de modéliser la houle. Ce modèle a pour expression :$ \nabla(CC_{g}\nabla(Ф))+k^{2}CC_{g}Ф = 0 $.
Nous utiliserons les notations suivantes :
ϕ : le potentiel
k : le nombre d’onde fonction de la profondeur H et de la fréquence ω (T est la période)

On a la relation implicite : $ ω^{2}=gktanh(kH) $
C : la célérité de l’onde
$ C_{g} $ : la célérité de groupe des vagues

Cas n°1 :

Nous sommes dans un domaine monodimensionnel plat de longueur L avec les conditions aux limites suivantes : $ Φ(x=0)=1 $ (condition de Dirichlet) et sortie libre amont $ \frac{\partial^{1}Φ(x=L)}{\partial x}=ikΦ(x=L) $ (condition de Robin).

On simplifie le problème en se plaçant dans le domaine des ondes longues : $ C=C_{g} $

On obtient donc : $ \frac{\partial^{2} Ф}{\partial x^2}+k^{2}Ф=0 $.

Résolution analytique :

Nous avons une équation homogène à coefficient constant : $ \frac{\partial^{2} Ф}{\partial x^2}+k^{2}Ф=0 $.

L'équation caractéristique est de la forme suivante : $ ax^{2}+bx+c=0 $. On calcule $ \Delta=-4k^{2} $.

On a : $ Φ(x) = Ae^{-ikx}+Be^{ikx} $ et $ \frac{\partial^{1}Φ(x)}{\partial x}=-ikAe^{-ikx}+ikBe^{ikx} $ avec (A,B) des constantes réelles à déterminer grâce aux conditions aux limites.

Conditions aux limites :

• $ Φ(x=0)=A+B=1 $, on a donc $ B = 1-A $.
• $ \frac{\partial^{1}Φ(x=L)}{\partial x} = ik(-Ae^{-ikL}+ikBe^{ikL})=ik(-Ae^{-ikL}+Be^{ikL}) $.

On a donc :

• $ A = 0 $
• $ B = 1 $

On obtient donc $ Φ(x)=e^{ikx} $.

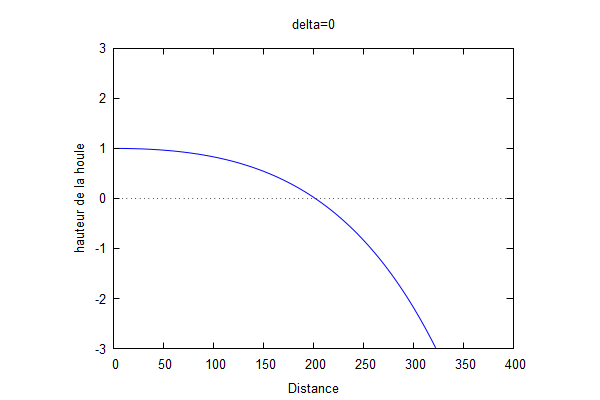
Au final : $ \color{red}Ф(x,t)=e^{i(kx-ωt)} $.

L'évolution de la hauteur de la houle au cours du temps correspond à l'équation suivante : $ \color{red}h(x,t)=Re(Ф(x,t))=cos(kx-ωt) $.

Résolution par la méthode d'homotopie

La relation d'homotopie est la suivante : $ (1−p)\frac{\partial^{2} Ф}{\partial x^{2}}+p(\frac{\partial^{2} Ф}{\partial x^{2}}+k^{2}Ф)=0 $

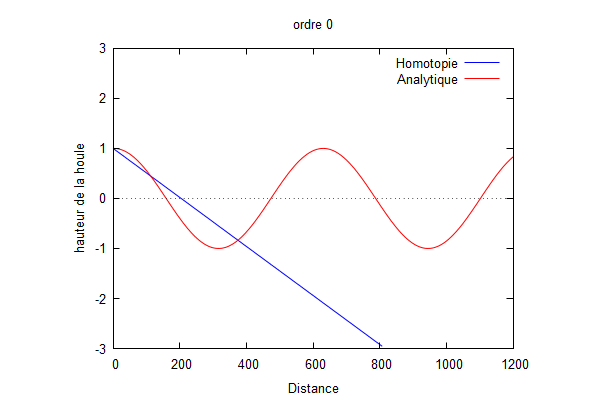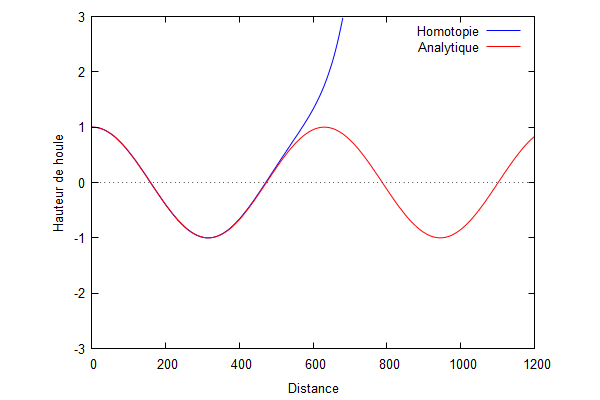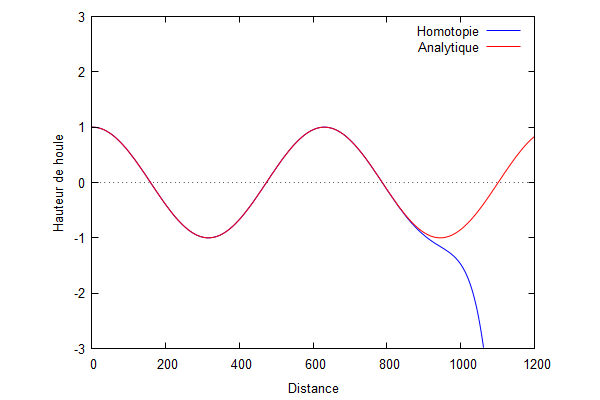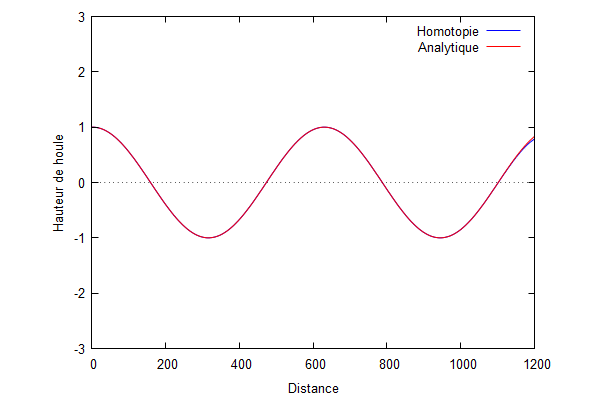
Ordre 0 :

On a : $ \frac{\partial^{2}Φ_{0}}{\partial x^{2}}=0 $

Donc $ Φ_{0}= Ax+B $ avec A et B deux constantes réelles à déterminer grâce aux conditions aux limites :

• $ Φ_{0}(x=0)=1 $ ↔ $ B=1 $
• $ Φ_{0}(x=L)=ikΦ_{0}(x=L) $ ↔ $ A=\frac{ik}{1-ikL} $

On a donc $ \color{red}Φ_{0}=\frac{ik}{1-ikL}x+1 $.

Ordre 1 :

On a : $ Ф_{1,xx}+k^{2}Ф_{0}=0 $ Donc : $ Ф_{1}=-k^{2}\iint(Ф_{0})+Ax+B $ avec A et B deux constantes réelles à déterminer grâce aux conditions aux limites :

• $ Ф_{1}(x=0)=0 $
• $ Ф_{1,x}(x=L)=ikФ_{1}(x=L) $.

On obtient donc : $ \color{red}Ф_{1}=-k^{2}\frac{ik}{6(1-ikL)}x^{3}+k^{2}\frac{1}{2}x^{2}-\frac{k^{2}L(k^{2}L^{2}+3ikL-3)}{3(1-ikL)^{2}}x $

Ordres supérieurs :

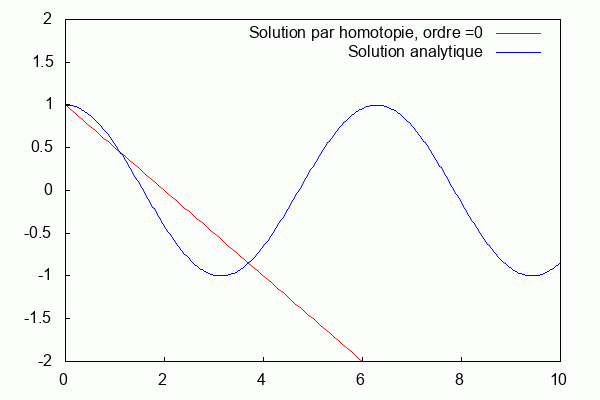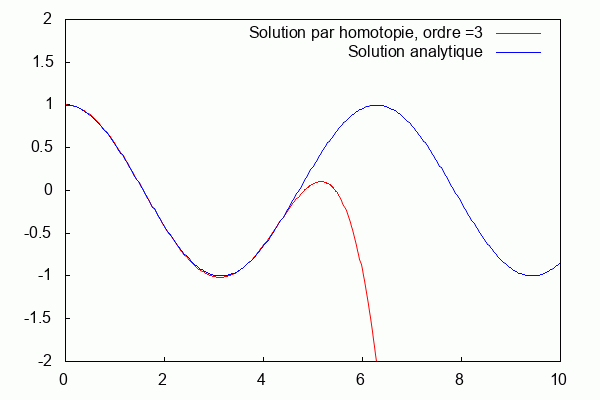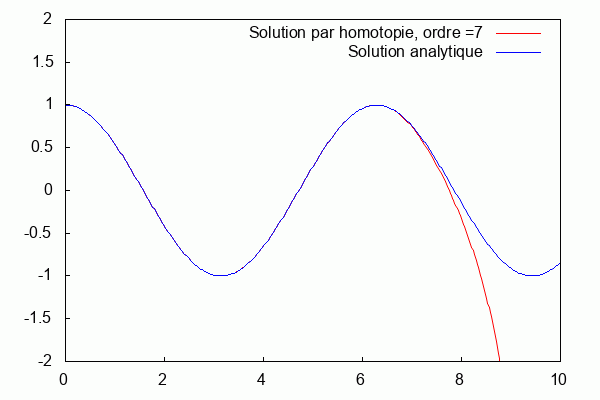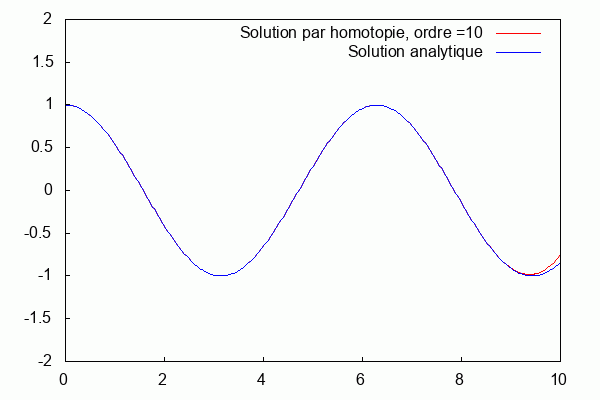
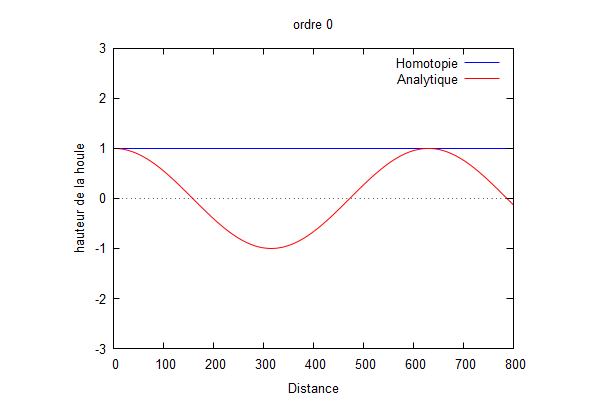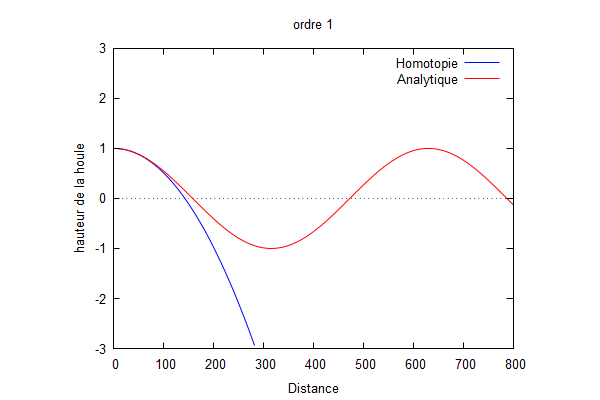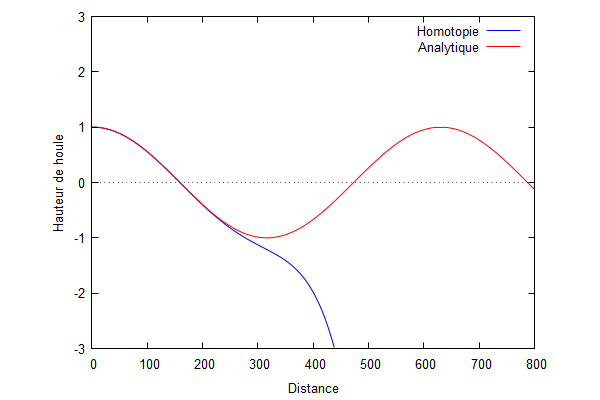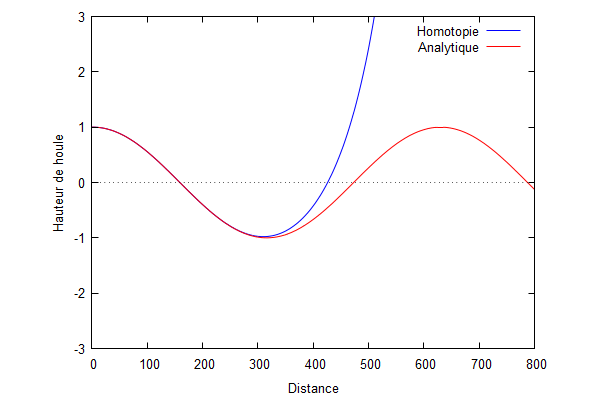
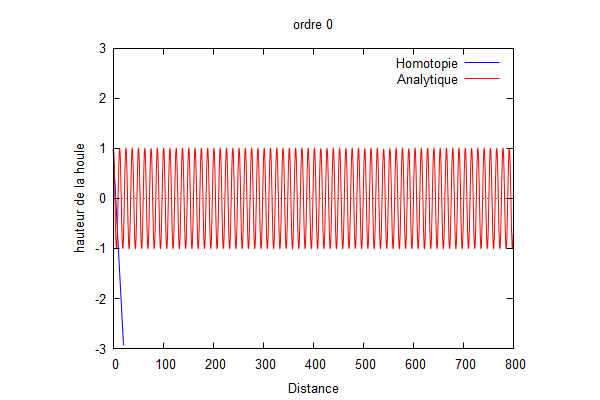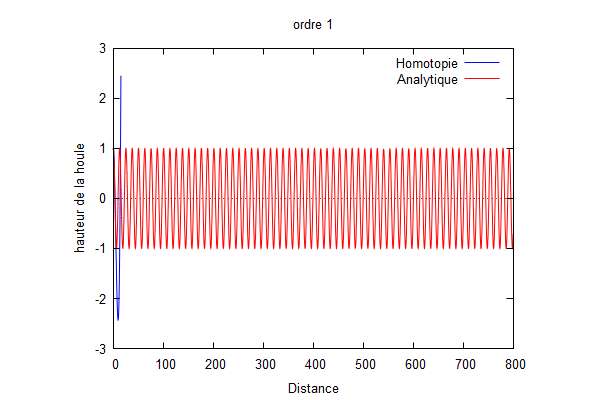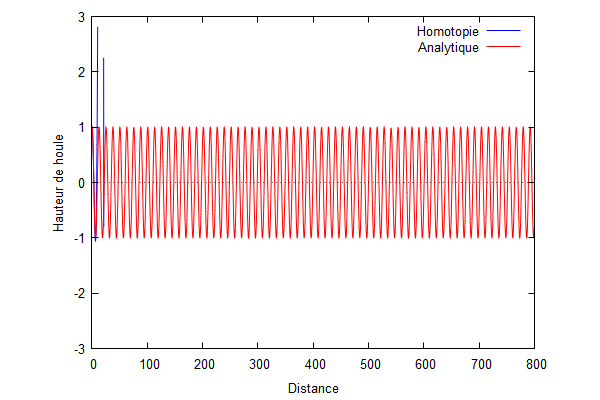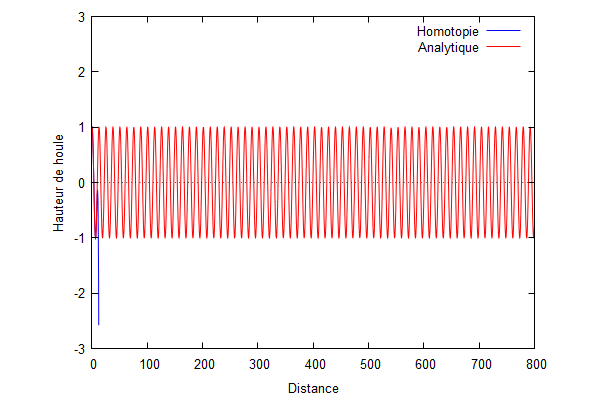
On utilise le logiciel wxmaxima afin de trouver Φ à tous les ordres.

Nous prenons : $ k=\frac{1}{100} $, $ L=\frac{1}{k} $

On superpose la solution analytique et la solution par homotopie.

Nous pouvons voir que la solution d'homotopie (courbe bleue) converge vers la solution analytique (courbe rouge) lorsque les ordres augmentent.

Cas n°2 :

Nous sommes dans le domaine monodimensionnel plat de longueur L avec les conditions aux limites suivantes : $ \frac{\partialΦ(x=0)}{\partial x}=ik(2-Φ(x=0)) $ en aval et $ \frac{\partialΦ(x=L)}{\partial x}=0 $ en amont.

Résolution analytique :

De la même manière que le cas n°1, le modèle de Berkhoff devient : $ \frac{\partial^{2} Ф}{\partial x^2}+k^{2}=0 $.

On obtient donc :

• $ \frac{\partialΦ(x=0)}{\partial x}=ik(-A+B)=ik(2-Φ(x=0))=ik(2-A-B) $ ↔ $ B=1 $
• $ \frac{\partialΦ(x=L)}{\partial x}=ik(-Ae^{-ikL}+Be^{ikL}=0 $ ↔ $ A=e^{2ikL} $.

On a donc : $ Φ(x)=e^{ik(2L-x)}+e^{ikx} $.

Au final : $ \color{red}Φ(x,t)=e^{i(-wt+k(2L-x))}+e^{kw-wt} $.

L'évolution de la hauteur de la houle au cours du temps correspond à l'équation suivante : $ \color{red}h(x,t)=Re(Ф(x,t))=cos(k(2L-x)-ωt)+cos(kx-wt) $.

Résolution par la méthode d'homotopie :

La relation d'homotopie est la suivante : $ (1−p)\frac{\partial^{2} Ф}{\partial x^2}+p(\frac{\partial^{2} Ф}{\partial x^2}+k^{2}Ф)=0 $. Mais dans ce cas n°2, les conditions aux limites sont différentes.

Ordre 0 :

On a $ Φ_{0,xx}=0 $ et donc $ Φ_{0}=Ax+B $.

Conditions aux limites :

• $ \frac{\partialΦ_{0,x}(x=L)}{\partial x}=0=A $.
• $ \frac{\partialΦ_{0,x}(x=0)}{\partial x}=ik(2-Φ(x=0))=ik(2-B)↔B=2 $.

On obtient ainsi : $ \color{red}Φ_{0}(x)=2 $.

Ordre 1 :

On a $ Φ_{1,xx}+k^{2}Φ_{0}=0 $ et donc $ Φ_{1}=-2k^{2}x^{2}+Ax+B $

Conditions aux limites :

• $ A=2k^{2}L $
• $ B=\frac{A}{-ik} $

On obtient ainsi : $ \color{red}Φ_{1}(x)=-k^{2}x^{2}+2k^{2}Lx+2ikL $.

Ordres supérieurs :

On utilise le logiciel wxmaxima afin de trouver Φ à tous les ordres.

On superpose la solution analytique et la solution par homotopie.

Nous prenons : $ k=\frac{1}{100} $, $ L=20 $

Nous pouvons voir que la solution d'homotopie (courbe bleue) converge vers la solution analytique (courbe rouge) lorsque les ordres augmentent.

Etude de la sensibilité de la solution en fonction du nombre d'onde du cas 1 et 2

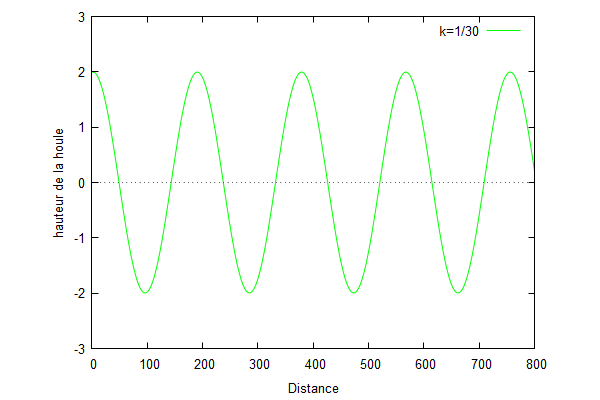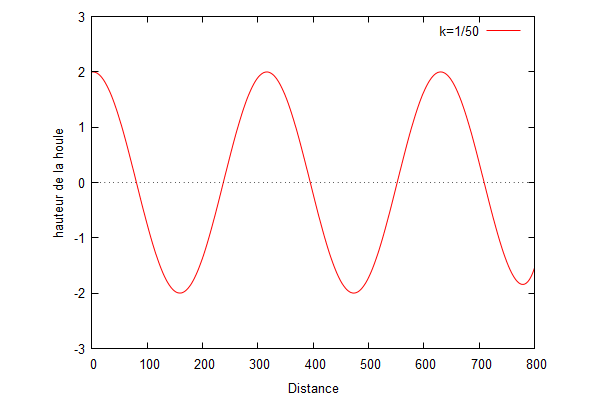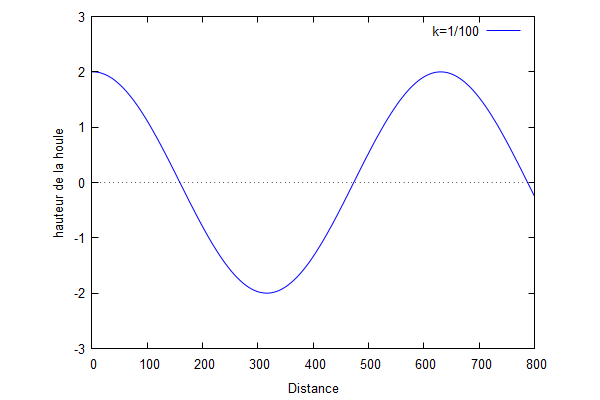
Nous traçons les courbes de l'équation de la hauteur de la houle en fonction de la distance en faisant varier le nombre d'onde. Nous prenons $ L=2 $

Cas 2

Nous pouvons voir que lorsque le nombre d'onde augmente, la fréquence des vagues augmentent et donc la période diminuent. Par conséquent, les vagues sont plus nombreuses mais plus petites lorsque le nombre d'onde augmente. Ces vagues parcourent de faible distance en raison de la dissipation d'énergie. Inversement, pour un faible nombre d'onde, les vagues sont plus longues et moins nombreuses et parcourent donc des distances plus importantes. En revanche, nous pouvons voir que la hauteur de la houle n'est pas modifiée lorsque l'on modifie le nombre d'onde.

De plus, en comparant avec la solution analytique, nous pouvons voir que lorsque k est petit ($ k<\frac{1}{L} $), la solution d'homotopie converge plus rapidement vers la solution analytique.

Cas 1 $ k=1/100 $ $ L=2 $

Cas 1 $ k=1/2 $ $ L=2 $

Réflexion portant sur l'analyse des résultats, les limites et l'intérêt de la méthode d'homotopie du cas 1 et 2

La méthode d'homotopie permet de déterminer les solutions du modèle à partir de solutions simples. Grâce au logiciel WXMAXIMA, nous avons pu tracer l'évolution de la hauteur de la houle en fonction du temps.

Grâce à ce modèle, nous étudions un cas simple de modélisation de la houle. En effet, nous avons fait l'hypothèse d'une onde monodimensionnelle alors qu'en réalité il s'agit d'une onde tridimensionnelle. De plus, de nombreux paramètres ne sont pas pris en compte : irrégularité des fonds océaniques (les fonds marins dessinent le relief à la surface des océans) et des littoraux. Nous ne prenons pas en compte l'érosion des roches sur les côtes.

Cas n°3

Nous sommes dans le domaine monodimensionnel plat de longueur L avec la pente du fond constante (s=cste) les conditions aux limites sont les suivantes $ Φ(x=0)=1 $ en aval et $ \frac{\partial^{1}Φ(x=L)}{\partial x})=ikΦ(x=L) $ en amont.

Le modèle de Berkhoff devient : $ H(x)Φ_{xx}-H'(x)Φ_{x}+k^{2}H(x)Φ=0 $ avec $ H(x)=H_{0}-sx $ et $ k=k0=constante $.

Résolution analytique

Nous avons effectuer le changement de variable suivant : $ z=H0-sx $ On a l'équation de Bessel suivante : $ z^{2}\frac{\partial^{2}Φ}{\partial z^{2}}+z\frac{\partial Φ}{\partial z}+z^{2}Φ=0 $

La solution de cette équation est de la forme suivante : $ Φ(x)=AJ_{0}(\sqrt{\frac{k}{s}z})+BY_{0}(\sqrt{\frac{k}{s}z}) $

On pose : $ z_{L}=\sqrt{\frac{k}{s}(H0-sL)} $ et $ z_{0}=\sqrt{\frac{k}{s}H0} $

On obtient :

• $ \color{red}A=\frac{iY_{0}(z_{L})-Y_{1}(z_{L})}{Y_{0}(z_{0})(J_{1}(z_{L})-iJ_{0}(z_{L})+J_{0}(z_{0})(iY_{0}(z_{L})-Y_{1}(z_{L}))} $
• $ \color{red}B=\frac{1}{Y_{0}(z_{0})+J_{0}(z_{0})\frac{iY_{0}(z_{L})-Y_{1}(z_{L})}{J_{1}(z_{L})-iJ_{0}(z_{L})}} $

Résolution par la méthode d′homotopie:

On a la relation d'homotopie suivante : $ (1-p)Φ_{xx}+p(H0-sx)Φ_{xx}-sΦ_{x}+k^2((H0-sx)Φ)=0 $

Ordre 0

On a : $ \frac{\partial^{2}Φ_{0}}{\partial x^{2}}=0 $

On a donc : $ Φ_{0}= Ax+B $

Avec les conditions initiales, on obtient : $ \color{red}Φ_{0}=\frac{ik}{1-ikL}x+1 $.

Ordre 1

On a : $ Φ_{1,xx}-Φ_{0,xx}+(1-εx)Φ_{0,xx}-sΦ_{0,x}+k^{2}(1-εx)Φ_{0}=0 $ avec $ ε=\frac{s}{H0} $.

On obtient donc : $ Φ_{1,xx}=Φ_{0,xx}-(1-εx)Φ_{0,xx}+sΦ_{0,x}-k^{2}(1-εx)Φ_{0} $

Donc $ Φ_{1}=\iint(sΦ_{0,x}-k^{2}(1-εx)Φ_{0})+Ax+B $.

Cas n°4

Nous sommes dans un canal monodimensionnel de largeur uniforme, de longueur L avec la forme du fond exponentielle. Les conditions aux limites sont les suivantes $ Φ(x=0)=1 $ en aval et $ \frac{\partial^{1}Φ(x=L)}{\partial x})=ikΦ(x=L) $ en amont.

Le modèle de Berkhoff devient : $ H(x)Φ_{xx}-H'(x)Φ_{x}+k^{2}H(x)Φ=0 $ avec $ H(x)=H0e^{-sx} $.

On a donc : $ Φ_{xx}-sΦ_{x}+k^{2}Φ=0 $

Résolution analytique

Dans ce cas n°4, $ H(x)=H0e^{-sx} $ et l'équation de Berkhoff devient : $ Φ_{xx}-sΦ(x)+k^{2}Φ(x)=0 $

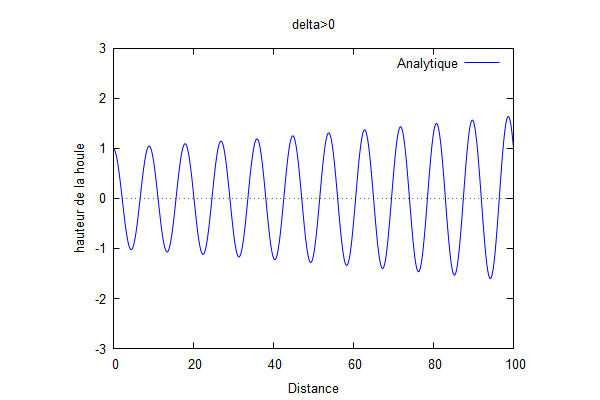
On calcule le discriminant : $ Δ=s^{2}-4k^{2} $. Nous avons pris pour chaque graphique : $ k=0.7 $ $ L=1/100 $

• Si $ Δ>0 $ :

On a deux racines réelles : $ x_{1}=\frac{s-\sqrt{s^{2}-4k^{2}}}{2} $ et $ x_{2}=\frac{s+\sqrt{s^{2}-4k^{2}}}{2} $

On a donc : $ Φ(x)=Ae^{\frac{s-\sqrt{s^{2}-4k^{2}}}{2}x}+Be^{\frac{s+\sqrt{s^{2}-4k^{2}}}{2}x} $.

Avec les conditions aux limites, on obtient : $ \color{red}Φ(x)=(1-\frac{x_{1}e^{x{1}L}-ike^{x_{1}L}}{x_{1}e^{x_{1}L}-ike^{x_{1}L}+x_{2}e^{x_{2}L}-ike^{x_{2}L}})e^{\frac{s-\sqrt{s^{2}-4k^{2}}}{2}x}+\frac{x_{1}e^{x{1}L}-ike^{x_{1}L}}{x_{1}e^{x_{1}L}-ike^{x_{1}L}+x_{2}e^{x_{2}L}-ike^{x_{2}L}}e^{\frac{s+\sqrt{s^{2}-4k^{2}}}{2}x} $.

• Si $ Δ=0 $ :

On a $ x_{0}=\frac{s}{2} $

On a donc : $ Φ(x)=(Ax+B)e^{\frac{sx}{2}} $

On obtient : $ \color{red}Φ(x)=(\frac{ik-x_{0}L}{1+Lx_{0}-ikL}x+1)e^{\frac{sx}{2}} $

• Si $ Δ<0 $ :

On a $ x_{1}=\frac{s-i\sqrt{-(s^{2}-4k^{2})}}{2} $ et $ x_{2}=\frac{s+i\sqrt{-(s^{2}-4k^{2})}}{2} $

On a donc : $ Φ(x)=e^{\frac{sx}{2}}(A\cos(\sqrt{\frac{-(s^{2}-4k^{2})}{2}}x)+B\sin(\sqrt{\frac{-(s^{2}-4k^{2})}{2}}x)) $

On note $ ν=\sqrt{\frac{-(s^{2}-4k^{2})}{2}} $

On obtient : $ \color{red}Φ(x)=e^{\frac{sx}{2}}(\cos(νx)+\frac{ν\sin(νL)+(ik-\frac{s}{2})\cos(νL)}{ν\cos(νL)+(\frac{s}{2}-ik)\sin(νL)}\sin(νx)) $

Résolution par la méthode d′homotopie:

On a la relation d'homotopie suivante : $ (1-p)Φ_{xx}+p(Φ_{xx}-spΦ_{x}+pk^2Φ)=0 $

Ordre 0

Comme pour le cas 3, on obtient : $ \color{red}Φ_{0}=\frac{ik}{1-ikL}x+1 $

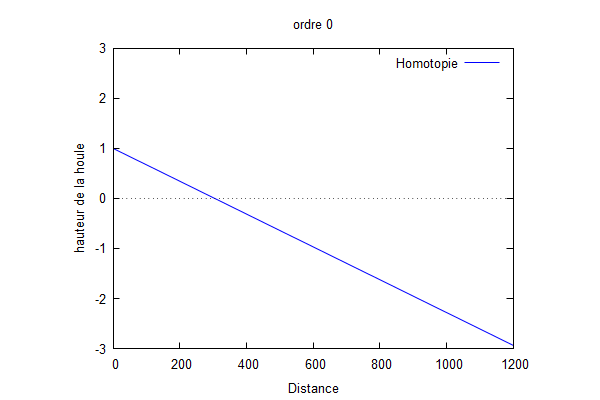Nous avons pris $ L=40 $ $ k=0.01 $

Ordre 1

Après calcul et simplification, on obtient : $ Φ_{1,xx}=sΦ_{0,x}-k^{2}Φ_{0} $

Pourquoi utiliser la méthode de l’homotopie ?

Dans notre problème de modélisation de la hauteur de la houle, il est plus facilement possible d’estimer une première solution que de trouver la solution exacte. La méthode de l’homotopie permet de partir de cette première solution relativement plus simple à identifier, et de trouver une solution exacte par convergence du modèle.

Ceci est rendu possible grâce à l’utilisation d’un paramètre qui varie entre 0 et 1 et qui assure la déformation continue entre la première estimation réalisée avec le paramètre valant 0 et la valeur finale de la solution avec la valeur du paramètre valant 1. Ceci permet d’atteindre la solution finale sans réaliser un très grand nombre d’itérations.

Domaine d'application du modèle

Actuellement, plus de 60% de la population mondiale vit dans la grande zone côtière, et près de 4 milliards d’individus sont donc installés à moins de 150 km d’une côte. Cette concentration d’habitants est en lien avec les enjeux sociaux et économique que représentent les fleuves, les mers et les océans. Le développement du tourisme balnéaire, des échanges par voies navigables a favorisé l’étude des caractéristiques physiques de la houle afin de mieux comprendre ce comportement dans l’objectif de pouvoir le prévoir.

Météo France

De même, de manière à pouvoir dimensionner les structures en mer, de connaître les conditions extrêmes et de pouvoir optimiser leur efficacité (on peut prendre par exemple le rendement des systèmes de récupération d’énergie), la modélisation de houle permet de calculer les interactions entre cette houle et ces structures présentent en mer ou sur les côtes.

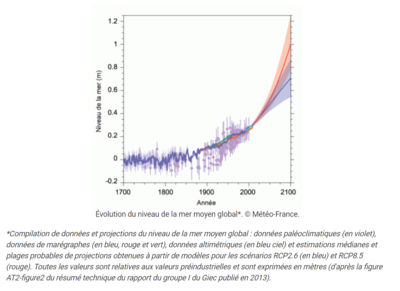
De plus, le changement climatique engendre de nouveaux effets sur la morphologie des littoraux, notamment ceux sableux qui dépendent de l’accélération de la montée du niveau de la mer, ainsi que de l’augmentation en fréquence ou en intensité de la force des tempêtes. Modéliser ce phénomène permet ainsi d’anticiper les risques futurs en variant les conditions initiales imposées sur la houle. En effet, l’érosion et la submersion marine sont susceptibles de croître du fait de cette élévation eustatique du niveau marin.

Le consortium IHES : une plateforme de récupération de l’énergie de la houle au large du Croisic

Limites du modèle

Notre modèle fonctionne ici à partir de plusieurs hypothèses qui limitent la précision de nos résultats. En effet, la mise en œuvre de ce modèle nécessite premièrement de faire des hypothèses en réalisant un ajustement des non-linéarités.

De plus, nous travaillons dans le cas d’un canal monodimensionnel dont le fond est soit plat dans les deux premiers cas, soit avec une pente qui possède une certaine régularité. Or dans la réalité, les fonds peuvent avoir de nombreuses irrégularités, et de plus, être chargés de sédiments – de toutes tailles allant du sable aux rochers – qui peuvent interférer avec les phénomènes de diffraction/réfraction. De même, cette interférence et modification des résultats peuvent avoir lieu du fait de l’irrégularité des traits de côtes, notamment au bord des océans et mer.

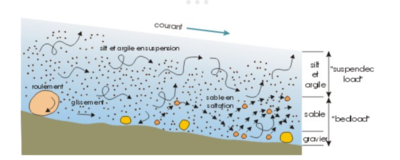Le courant transporte toute tailles de sédiments qui peuvent impacter les phénomènes de houle

L’irrégularité des traits et principalement dû à une érosion différentielle, qui provient de la constitution des roches, mais également de la vitesse es vagues qui n’est ici pas pris en compte mais qui rentre en jeu dans les submersions marines.

Il peut également être à noter que le trafic maritime peut avoir un impact sur la création de vagues et donc sur la régularité ou l’irrégularité, l’intensité et la fréquence de la houle sur les côtes, notamment dans les canaux créés pour le transport maritime.

On peut enfin noter également des limites mathématiques du modèle, notamment sur l’utilisation de constantes telles que k, L et oméga, qui sont certainement loin d’être constante dans la réalité mais qui permettent de simplifier ce modèle et d’obtenir une idée globale du résultat. De même, la houle dépend du vent, des courants, et varie dans le temps alors qu’on la considère ici comme un phénomène constant.