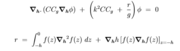Utilisateur:Jean-Michel Tanguy/SujetENTPE2020/DE MACEDO ANGELICO // DREVON // GATOUILLAT

Bon courage et n'hésitez pas à communiquer avec moi par mail: jm.tanguy@shf-hydro.org

Mise en contexte

• Dans une situation d'urgence climatique, certains territoires ainsi que leurs populations, sont sujets à de véritables enjeux, notamment les territoires le long des côtes. En effet, les littoraux font l'objet de préoccupations majeures en ce qui concerne le devenir des populations et l'augmentation du niveau des océans. C'est pourquoi il est particulièrement intéressant de pouvoir quantifier l'impact des houles sur le territoire.
• Au cours de cette étude, nous modéliserons la houle avec le modèle de Berkhoff :
  
• Utilisation de la méthode d'homotopie : A partir d'une solution simple relativement connue, on converge vers une solution finale complète. On choisit la dérivée seconde comme fonction auxiliaire et on part d'une solution initiale unitaire. Introduire un paramètre p permet d'assurer la continuité de la déformation. Il existe la possibilité de résoudre les équations différentielles au moyen de logiciel de programmation.
  
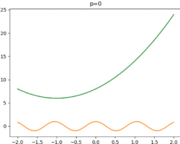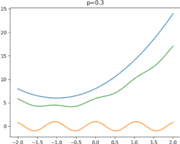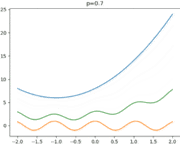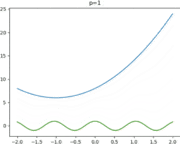
• Visualisation du principe d'homotopie : lorsque p = 0 la courbe représente la solution initiale. On peut ensuite constater l'évolution de la courbe qui converge vers la solution finale quand p tend vers 1.

Modélisation graphique du principe d'homotopie.

Cas n°1

Hypothèses et conditions aux limites

On considère un domaine monodimensionnel plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire ϕ=1 et sortie libre amont ϕx=ikϕ. On impose ces 2 conditions limites en x=0. On peut montrer que cela est équivalent au cas où les 2 conditions limites sont imposées aux 2 extrémités du domaine, x=0 et x=L.

Solution analytique

Dans ce premier cas, on considère que la profondeur H est constante. On a alors l'équation de Berkhoff suivante :
$ \frac{\partial^2 Φ}{\partial x^2}+k^2Φ(x)=0 $

On calcule le discriminant $ Δ = -4k^2 $ et les racines $ r+ = ik $ & $ r- = -ik $
On obtient donc $ Φ = A*exp(-ikx) + B*exp(ikx) $

En utilisant les conditions initiales, on a :

 - $ Φ(0) = 1 $ donc $ A + B = 1 $ 

 - $ \frac{\partial^1 Φ}{\partial x^1}(x=L) = ikΦ(x=L) $ donc $ A = 0 $ 

On obtient donc finalement $ \boxed{Φ(x) = exp(ikx)} $

On peut ainsi déduire de ce résultat :

 - $ Re(Φ(x)) = cos(kx) $  

 - $ |Φ(x)| = 1 $ 

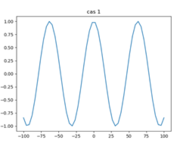
On en déduit la hauteur de houle $ \boxed{H(x) = cos(kx)} $

On peut également déduire sa variation temporelle : $ Φ(x,t) = exp(i(kx-wt)) $ d'où $ \boxed{h(x,t) = cos(kx-wt)} $

Représentation graphique de la solution analytique (cas n°1).

Homotopie

On a l'équation de Berkhoff suivante : $ \frac{\partial^2 Φ}{\partial x^2}+k^2Φ(x)=0 $
On obtient ainsi la relation d'homotopie suivante : $ (1-p)*(Φxx - u0xx) + p*(Φxx + k²*Φ) = 0 $
Donc $ Φxx - u0xx + p*u0xx + p*k²*Φ = 0 $

À l'ordre 0, on a :
$ Φ0xx - u0xx = 0 $ donc $ Φ0 - u0 = A*x + B $
avec $ Φ0(0) = 1 $ donc $ B = 0 $ et $ Φ0x(L) = i*k*Φ0(L) $ donc $ A = \frac{i*k}{1 - i*k*L} $
On a donc finalement $ \boxed{Φ0(x) = \frac{i*k}{1 - i*k*L}*x + 1} $

Donc : $ \boxed{h_0(x,t) = 2\frac{cos(wt)(\frac{-kx}{2}+1)-kxsin(wt)}{\sqrt{(-kx+2)²+(kx)²}}} $

À l'ordre 1, on a :
$ Φ1xx + u0xx + k²*Φ0 = 0 $ donc $ Φ1 = A*x + B -4 - k²*{\displaystyle \textstyle \int }{\displaystyle \textstyle \int }Φ0 $
avec $ {\displaystyle \textstyle \int }{\displaystyle \textstyle \int }Φ0 = \frac{i*k}{6(1-i*k*L)}*x^3 - \frac{k²}{2)}*x² - k²*C1*x - k²*C2 $
On a finalement $ \boxed{Φ1(x) = \frac{-ik^3}{6(1-ikL)}x^3-\frac{k²}{2}x²+\frac{x}{1-ikL}(\frac{k^4L^3}{6(1-ikL)}-\frac{ik^3(5-3ikL)L²}{6}+k²L+1)+1} $

Donc : $ \boxed{h_1(x,t) = \frac{cos(wt)(\frac{k^3x^3}{12}+\frac{-k²x²}{2}+\frac{2kx}{3}+\frac{x}{2})-sin(wt)(-\frac{k^3x^3}{12}-\frac{kx}{12}+\frac{x}{2})}{\sqrt{(\frac{k^3x^3}{12}+\frac{-k²x²}{2}+\frac{2kx}{3}+\frac{x}{2})²+(-\frac{k^3x^3}{12}-\frac{kx}{12}+\frac{x}{2})²}}} $

À l'ordre 2, on a :
$ Φ2xx + k²*Φ1 = 0 $ d'où $ Φ2 = A*x + B - k²*{\displaystyle \textstyle \int }{\displaystyle \textstyle \int }Φ1 $

En posant $ a = \frac{1}{1-ikL}(\frac{k^4*L^3}{6(1-ikL)}-\frac{ik^3*L^2*(5-3ikL)}{6}-k²L + 1) $ et $ b = \frac{1}{1-ikL}*(\frac{k^6*L^5}{120(1-ikL)} + ik^5*L^4*(\frac{1}{1-ikL}-\frac{1}{24}) + ikL^3*(\frac{k^3}{6} + \frac{a}{6}) + \frac{k*L^2}{2}*(i-k*a) - k²L + 1 $

On obtient $ {\displaystyle \textstyle \int }{\displaystyle \textstyle \int }Φ1 = \frac{-i*k^3}{120(1-i*k*L)}*x^5 - \frac{k²}{24}*x^4 +\frac{a}{6}*x^3 + \frac{1}{2}*x² + C1*x + C2 $
On a finalement $ \boxed{Φ2(x) = \frac{-ik^5}{120(1-ikL)}*x^5 - \frac{k^4}{24}*x^4 + \frac{a}{6}*x^3 + \frac{1}{2}*x² + b*x + 1} $

Donc : $ \boxed{h_2(x,t) = \frac{cos(wt)(\frac{k^5x^5}{240}+\frac{k^4x^4}{24}+x^3(\frac{k}{18}+\frac{1}{12})+\frac{x²}{2}+x(\frac{17L}{144}-\frac{3k}{16}-\frac{L²}{12}-\frac{17k}{16}-\frac{L}{4}+\frac{1}{2})+1)-sin(wt)(\frac{-k^5x^5}{240}-\frac{13kx^3}{72}+\frac{x^3}{12}+x(\frac{L}{16}+\frac{17k}{48}-\frac{1}{4}-\frac{13k}{30}-\frac{L}{4}+\frac{1}{2}))}{\sqrt{(\frac{k^5x^5}{240}+\frac{k^4x^4}{24}+x^3(\frac{k}{18}+\frac{1}{12})+\frac{x²}{2}+x(\frac{17L}{144}-\frac{3k}{16}-\frac{L²}{12}-\frac{17k}{16}-\frac{L}{4}+\frac{1}{2})+1)²+(\frac{-k^5x^5}{240}-\frac{13kx^3}{72}+\frac{x^3}{12}+x(\frac{L}{16}+\frac{17k}{48}-\frac{1}{4}-\frac{13k}{30}-\frac{L}{4}+\frac{1}{2}))²}}} $

Finalement, par homotopie, on obtient : $ \boxed{h(x,t) = \frac{cos(wt)(\frac{-kx}{2}+1+\frac{k^3x^3}{12}+\frac{-k²x²}{2}+\frac{2kx}{3}+\frac{x}{2}+\frac{k^5x^5}{240}+\frac{k^4x^4}{24}+x^3(\frac{k}{18}+\frac{1}{12})+\frac{x²}{2}+x(\frac{17L}{144}-\frac{3k}{16}-\frac{L²}{12}-\frac{17k}{16}-\frac{L}{4}+\frac{1}{2})+1)-sin(wt)(kx-\frac{k^3x^3}{12}-\frac{kx}{12}+\frac{x}{2} + \frac{-k^5x^5}{240}-\frac{13kx^3}{72}+\frac{x^3}{12}+x(\frac{L}{16}+\frac{17k}{48}-\frac{1}{4}-\frac{13k}{30}-\frac{L}{4}+\frac{1}{2}))}{\sqrt{(\frac{-kx}{2}+1+\frac{k^3x^3}{12}+\frac{-k²x²}{2}+\frac{2kx}{3}+\frac{x}{2}+\frac{k^5x^5}{240}+\frac{k^4x^4}{24}+x^3(\frac{k}{18}+\frac{1}{12})+\frac{x²}{2}+x(\frac{17L}{144}-\frac{3k}{16}-\frac{L²}{12}-\frac{17k}{16}-\frac{L}{4}+\frac{1}{2})+1)^2+(kx-\frac{k^3x^3}{12}-\frac{kx}{12}+\frac{x}{2} + \frac{-k^5x^5}{240}-\frac{13kx^3}{72}+\frac{x^3}{12}+x(\frac{L}{16}+\frac{17k}{48}-\frac{1}{4}-\frac{13k}{30}-\frac{L}{4}+\frac{1}{2}))^2}}} $

Cas n°2

Hypothèses et conditions aux limites

Domaine monodimensionnel plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire et une condition de flux aval ϕx=ik(2−ϕ) et réflexion totale amont ϕx=0 .
Utilisation de la méthode standard

Solution analytique

Dans ce second cas, on considère toujours que la profondeur H est constante. On a alors la même équation de Berkhoff que dans le cas 1 :
$ \frac{\partial^2 Φ}{\partial x^2}+k^2Φ(x)=0 $

De la même façon, on obtient $ Φ = A*exp(-ikx) + B*exp(ikx) $

En utilisant les conditions initiales, on a :

 - $ \frac{\partial^1 Φ}{\partial x^1}(L) = 0 $ donc $ B = 1 $ 

 - $ \frac{\partial^1 Φ}{\partial x^1}(0) = ik*(2-Φ(0)) $ donc $ A = exp(2ikL) $ 

On obtient donc finalement $ \boxed{Φ(x) = exp(ik(2L-x)) + exp(ikx)} $

On peut ainsi déduire de ce résultat :

 - $ Re(Φ(x)) = cos(k(2L-x)) + cos(kx) $ 

 - $ |Φ(x)| = 2 + 2(cos(k(2L-x))cos(kx) + sin(k(2L-x))sin(kx)) $ 

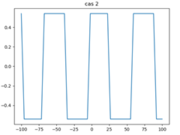
On en déduit la hauteur de houle $ \boxed{H = \frac{cos(k(2L-x)) + cos(kx)}{2 + 2cos(2k(L-x))}} $

On peut également déduire sa variation temporelle : $ Φ(x,t) = exp(i(k(2L-x)-wt))+exp(i(kx-wt)) $ d'où $ \boxed{h(x,t) = \frac{cos(k(2L-x)+wt) + cos(kx+wt)}{\sqrt{2 + 2cos(2k(L-x))}} } $

Représentation graphique de la solution analytique (cas n°2).

Homotopie

Comme l'équation de Berkhoff est identique à celle du cas 1, la relation d'homotopie l'est également :
$ Φxx - u0xx + p*u0xx + p*k²*Φ = 0 $

À l'ordre 0, on a :
$ Φ0xx - u0xx = 0 $ donc $ Φ0 = A*x + B + 1 $ avec $ Φ0x(L) = A = 0 et Φ0x(0) = ik(2-Φ0(L)) $ donc $ B = 1 $
On a donc finalement $ \boxed{Φ0(x) = 2} $

Donc : $ \boxed{h_0(x,t) = cos(wt} $

À l'ordre 1, on a :
$ Φ1xx + u0xx + k²*Φ0 = 0 $ donc $ Φ1 = A*x + B -1 - k²*{\displaystyle \textstyle \int }{\displaystyle \textstyle \int }Φ0 $ avec $ {\displaystyle \textstyle \int }{\displaystyle \textstyle \int }Φ0 = x² + C1*x + C2 $
En utilisant les conditions aux limites, on obtient : $ A - k²*C1 = 2Lk² $ et $ B - k²*C2 = 2 + 2ikL $
On a finalement $ \boxed{Φ1(x) = -k²*x² + 2Lk²x + 2ikL + 2 } $

Donc : $ \boxed{h_1(x,t) = \frac{cos(wt)(-k²x²+2kx+2)-2sin(wt)}{\sqrt{(-k²x²+2kx+2)²+ 4}}} $

À l'ordre 2, on a :
$ Φ2xx + k²*Φ1 = 0 $
donc $ Φ2 = A*x + B - k²*{\displaystyle \textstyle \int }{\displaystyle \textstyle \int }Φ1 $ avec $ {\displaystyle \textstyle \int }{\displaystyle \textstyle \int }Φ1 = \frac{-k²}{12}x^4 + \frac{2Lk²}{6}x^3 + (1+ikL)x² + C1x + C2 $
En utilisant les conditions aux limites, on obtient : $ A - k²*C1 = \frac{-k^4}{3}L^3 + k^4*L² + ikL + 1 $ et $ B - k²*C2 = L²+2 - iL(\frac{k^3}{3}L² - Lk^3 + \frac{1}{k}) $
On a finalement $ \boxed{Φ2(x) = \frac{k^4}{12}x^4 - \frac{Lk^4}{3}x^3 + (ikL+1)x² - L(\frac{k^4}{3}L² - Lk^4 + ikL + 1)x + 2 + L² - iL(\frac{k^3}{3}L² - Lk^3 + \frac{1}{k})}( $

Donc : $ \boxed{h_2(x,t) = \frac{cos(wt)(\frac{k^4x^4}{12}-\frac{k^3x^3}{3}+x²-x(\frac{k}{3}-k²+L)+2+L²)-sin(wt)(x²-L+k-L²-\frac{1}{3})²)}{\sqrt{(\frac{k^4x^4}{12}-\frac{k^3x^3}{3}+x²-x(\frac{k}{3}-k²+L)+2+L²)²+(x²-L+k-L²-\frac{1}{3})²}}} $

Finalement, par homotopie, on obtient : $ \boxed{h(x,t) = \frac{cos(wt)(1-k²x²+2kx+2+\frac{k^4x^4}{12}-\frac{k^3x^3}{3}+x²-x(\frac{k}{3}-k²+L)+2+L²)-sin(wt)(2+x²-L+k-L²-\frac{1}{3})}{\sqrt{(1+-k²x²+2kx+2+\frac{k^4x^4}{12}-\frac{k^3x^3}{3}+x²-x(\frac{k}{3}-k²+L)+2+L²)^2+(2+x²-L+k-L²-\frac{1}{3})^2}}} $

Représentation graphique de la solution homotopie (cas n°2).

Cas n°3

Hypothèses et conditions aux limites

Domaine monodimensionnel de longueur L avec pente du fond constante avec entrée par l'aval d'une onde de fréquence unitaire ϕ=1 sortie libre amont ϕx=ikϕ
On considèrera que le nombre d'onde k est constant.

Solution analytique

On considère que la profondeur H(x) est linéaire de pente a : $ H(x) = H_0 - ax $
On obtient alors l'équation de Berkhoff suivante : $ (H_0 - ax)\frac{\partial^2 Φ}{\partial x^2} - a\frac{\partial Φ}{\partial x} + k²(H_0 - ax)Φ = 0 $
Pour la résoudre, on effectue le changement de variable $ X = \frac{k}{a}(H_0 - ax) $
On obtient alors l'équation de Bessel suivante : $ X²\frac{\partial^2 Φ}{\partial x^2} + X\frac{\partial Φ}{\partial x} + X²Φ = 0 $

La solution est donc de la forme $ Φ(X) = A*J_0(X) + B*Y_0(X) $ où $ J_0 $ est la fonction de Bessel de première espèce et $ Y_0 $ la fonction de Bessel de seconde espèce.
En utilisant les conditions aux limites et en posant $ X_0 = \frac{k}{a}H_0 $ et $ X_L = \frac{k}{a}(H_0 - aL) $, on obtient :
$ A = \frac{aY_1(X_L)+bY_0(X_L)+i(aY_0(X_L)-bY_1(X_L))}{a²+b²} $ et $ B = \frac{aJ_1(X_L)+bJ_0(X_L)+i(aJ_0(X_L)-bJ_1(X_L))}{a²+b²} $
avec $ a = J_1(X_L)Y_0(X_0)-J_0(X_0)Y_1(X_L) $ et $ b = J_0(X_L)Y_0(X_0)-J_0(X_0)Y_0(X_L) $

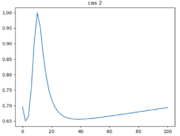
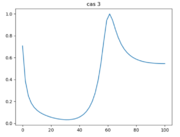
On obtient donc $ \boxed{Φ(x,t) = (AJ_0(\frac{k}{a}(H_0 - ax)) + BY_0(\frac{k}{a}(H_0 - ax)))e^{-iwt}} $

On peut donc conclure avec l'évolution temporelle de la hauteur de houle $ \boxed{h(x,t) = \frac{cos(wt)(Re(A)J_0(\frac{k}{a}(H_0 - ax)) + Re(B)Y_0(\frac{k}{a}(H_0 - ax)))-sin(wt)(Im(A)J_0(\frac{k}{a}(H_0 - ax))+Im(B)Y_0(\frac{k}{a}(H_0 - ax)))}{\sqrt{(\Re(A)J_0(\frac{k}{a}(H_0-ax))+\Re(B)Y_0(\frac{k}{a}(H_0-ax)))^2+(\Im(A)J_0(\frac{k}{p}(H_0-ax))+\Im(B)Y_0(\frac{k}{a}(H_0-ax)))^2}}} $

Homotopie

En posant $ e = \frac{a}{H_0} $, on obtient la relation d'homotopie suivant : $ Φxx - pe*x*Φxx - pe*Φx + pk²(1-e*x)Φ = 0 $

À l'ordre 0, on a :
$ Φ0xx = 0 $ donc $ Φ0 = A*x + B $ avec $ Φ0(0) = 1 = B et Φ0x(L) = ikΦ0(L) $ donc $ A = \frac{ik}{1-ikL} $
On a donc finalement $ \boxed{Φ0(x) = \frac{ik-k²L}{1+(kL)²}x + 1} $

Donc : $ \boxed{h_0(x,t) = 2\frac{cos(wt)(\frac{-kx}{2}+1)-kxsin(wt)}{\sqrt{(-kx+2)²+(kx)²}}} $

À l'ordre 1, on a :
$ Φ1xx - ex*Φ0xx - eΦ0x + k²(1-ex)Φ0 = 0 $. Posons $ \alpha = \frac{ik-k²L}{1+(kL)²} $ et $ \gamma = i\alpha = \frac{-k-ik²L}{1+(kL)²} $
On a $ \boxed{Φ1(x) = Ax + B + k²e\alpha\frac{x^4}{12} - k²(\alpha + e)\frac{x^3}{6} + (e\alpha - k²)\frac{x²}{2}} $

avec $ B = 1 $ et $ A = \frac{12+e\gamma*k^3L^4+6k(e\gamma-ik²)L²-4k^2e\alpha*L^3+6k²(\alpha+e)L²-12(e\alpha-k²)L+kL(12i-k^3eL^4\alpha+2k^3(\alpha+e)L^3+6k(k²-e\alpha)L²-4k²e\gamma*L^3+6k²(\gamma+ie)L^3-12(e\gamma+ik²)L²)}{12(1+(kL)²)} $

Donc : $ \boxed{h_1(x,t) = \frac{cos(wt)(\frac{ek^3x^4}{24}-\frac{k^3x^3}{12}+\frac{ekx^2}{4}+(-\frac{e}{8}+\frac{Le}{4}-\frac{5e}{12}-\frac{1}{8}-\frac{5k}{24}+\frac{Le}{4})x)-sin(wt)(\frac{-ek^3x^4}{24}+x^3(\frac{k^3}{12}-\frac{ek^2}{6})+x^2(\frac{-k^2}{2}-\frac{ek}{4})+x(\frac{-e}{8}+\frac{eL}{4}+\frac{13e}{24}-\frac{1}{8}+\frac{17k}{24}+\frac{e}{12}+\frac{1}{2})+1)}{\sqrt{(\frac{ek^3x^4}{24}-\frac{k^3x^3}{12}+\frac{ekx^2}{4}+(-\frac{e}{8}+\frac{Le}{4}-\frac{5e}{12}-\frac{1}{8}-\frac{5k}{24}+\frac{Le}{4})x)²+(\frac{-ek^3x^4}{24}+x^3(\frac{k^3}{12}-\frac{ek^2}{6})+x^2(\frac{-k^2}{2}-\frac{ek}{4})+x(\frac{-e}{8}+\frac{eL}{4}+\frac{13e}{24}-\frac{1}{8}+\frac{17k}{24}+\frac{e}{12}+\frac{1}{2})+1)²}}} $

Finalement, par homotopie, on obtient : $ \boxed{h(x,t) = \frac{cos(wt)(\frac{-kx}{2}+1+\frac{ek^3x^4}{24}-\frac{k^3x^3}{12}+\frac{ekx^2}{4}+(-\frac{e}{8}+\frac{Le}{4}-\frac{5e}{12}-\frac{1}{8}-\frac{5k}{24}+\frac{Le}{4})x)-sin(wt)(kx+\frac{-ek^3x^4}{24}+x^3(\frac{k^3}{12}-\frac{ek^2}{6})+x^2(\frac{-k^2}{2}-\frac{ek}{4})+x(\frac{-e}{8}+\frac{eL}{4}+\frac{13e}{24}-\frac{1}{8}+\frac{17k}{24}+\frac{e}{12}+\frac{1}{2})+1)}{\sqrt{(\frac{-kx}{2}+1+\frac{ek^3x^4}{24}-\frac{k^3x^3}{12}+\frac{ekx^2}{4}+(-\frac{e}{8}+\frac{Le}{4}-\frac{5e}{12}-\frac{1}{8}-\frac{5k}{24}+\frac{Le}{4})x)^2+(kx+\frac{-ek^3x^4}{24}+x^3(\frac{k^3}{12}-\frac{ek^2}{6})+x^2(\frac{-k^2}{2}-\frac{ek}{4})+x(\frac{-e}{8}+\frac{eL}{4}+\frac{13e}{24}-\frac{1}{8}+\frac{17k}{24}+\frac{e}{12}+\frac{1}{2})+1)^2}}} $

Représentation graphique de la solution homotopie(cas n°3).

Cas n°6

Hypothèses et conditions aux limites

On étudie cette fois un domaine bidimensionnel avec une bosse immergée parabolique sur le fond. On mènera l'étude en coordonnées polaire et cartésienne.

Solution analytique

En nous munissant d'un repère en coordonnées polaires (O,e_r,e_θ), on trouve l'équation de Berkhoff suivante :
$ \frac{\partial Φ \partial H}{\partial r^2} + \frac{1}{r^2}\frac{\partial Φ \partial H}{\partial θ^2} + H*(\frac{1}{r^2}\frac{\partial^2 Φ}{\partial θ^2} + \frac{1}{r}\frac{\partial Φ}{\partial r} + \frac{\partial^2 Φ}{\partial r^2} + k^2*Φ)=0 $

En nous munissant d'un repère en coordonnées carthésiennes (O,e_x,e_y), on trouve l'équation de Berkhoff suivante :
$ \frac{\partial Φ \partial H}{\partial x^2} + \frac{\partial Φ \partial H}{\partial y^2} + H*(\frac{\partial^2 Φ}{\partial x^2} + \frac{\partial^2 Φ}{\partial y^2} + k^2*Φ)=0 $

La solution analytique étant difficile à obtenir, on applique à la place la méthode d'homotopie qui permettra quant à elle d'obtenir une approximation analytique.

Étude de sensibilité

Les approximations réalisées ont des conséquences sur les résultats obtenus. Ils sont plus ou moins proches de ce que l'on peut réellement observer sur les littoraux. Les approximations faites pour créer des modèles assez réalistes mais qui restent simples, négligent quelques paramètres, notamment les facteurs qui influencent la croissance des vagues comme :

- la hauteur, la période et la direction des vagues existantes 

- l'angle entre la direction du vent et celles des vagues 

- le ratio de la vitesse du vent à la vitesse de phase (la vitesse de phase étant la vitesse de déplacement des crêtes de vagues) 

- la durée de l'action du vent 

- la force et la fréquence des rafales 

- les courants marins 

- les marées 

- les interactions des vagues entre-elles 

De manière générale, en nous concentrant sur les outils dont nous disposons pour nos calculs, on peut déjà remarquer quelques points. Premièrement, nous avons considérer le nombre d'onde k constant. Or ce nombre, proportionnel à l'inverse de la longueur d'onde, n'est absolument pas constant pour ces phénomènes naturels (la longueur d'onde des vagues n'est jamais exactement identique). Ensuite, le fond de l'estuaire est très difficile à modéliser par rapport à sa complexité : sa pente comporte de nombreuses singularités qui auront une influence importante sur la houle.

Cas n°1 :

Les hypothèses pour le cas n°1 sont très simplifiées, puisqu'il constitue une entrée en matière du sujet, donc les résultats obtenus sont extrêmement biaisés. En effet, le fond de l'estuaire n'est en réalité absolument pas plat et contient de nombreuses irrégularités. De plus, une étude monodimensionnel ne peut être qu'incomplète dans une étude comme celle-ci. Enfin, les conditions aux limites sont largement simplifiées également.

Cas n°2 :

Les hypothèses sont encore largement simplifiées. Le fond de l'estuaire n'est pas plat : il est en réalité en pente et comporte de nombreuses irrégularités. L'étude monodimensionnelle n'est pas adaptée pour une telle étude. De plus, la condition aux limites de réflexion totale de l'onde en aval est largement simplifiée puisqu'en réalité l'onde n'est pas complètement réfléchie.

Cas n°3 :

Les hypothèses de ce cas le rapproche d'une réalité largement simplifiée : une pente linéaire s'assimile plus facilement à la réalité du fond de l'estuaire. Mais cependant les irrégularités sont négligées et la pente d'un estuaire ne peut se réduire à un modèle strictement linéaire. De plus, les conditions aux limites sont largement simplifiées.

Cas n°6 :

Les hypothèses correspondent un peu plus aux cas réels, c'est à dire avec un fond qui n'est pas plat mais qui présente des irrégularités comme une bosse. De plus, une étude bidimensionnelle semble plus adéquate pour ce type d'étude. Cependant, la pente est considérée comme nulle. On pourrait ainsi approfondir cette modélisation avec une pente linéaire voire une pente exponentielle. On pourrait également complexifier d'avantage en prenant en compte plusieurs des phénomènes naturels énoncés plus haut influençant la modélisation .

Analyse des résultats

Résultats numériques

La modélisation de la houle (donc les différents trains d'ondes de fréquences et de directions différentes) ne se base en réalité pas sur une onde unique mais sur l'évolution de l'énergie des vagues : on étudie le spectre de la houle plutôt qu'une onde unique. Pour représenter la houle au plus près de la réalité, on utilise une méthode que l'on appelle houle aléatoire (approche statistique et spectrale).

Il est évident que les résultats que nous avons obtenus sont assez éloignés des phénomènes réels.

Prolongement de l'étude de la quantification des houles sur le littoral

On peut améliorer la méthode en utilisant une version plus précise de l'équation de Berkhoff : L'équation "mild-slope étendue" représente une version instationnaire de l'équation originale de Berkhoff et permet de modéliser des houles qui ne sont pas nécessairement linéaires ou stationnaires. De même, l'équation du nom de "mild-slope modifiée" permet de considérer des variations topographiques plus grandes et plus rapides.

Équation mild-slope étendue.

Équation mild-slope modifiée.

source : Jenna Charland. Modélisation de la propagation de la houle en présence d'un courant inhomogène et au-dessus d'une topographie variable. Autre [cond-mat.other]. Université de Toulon, 2014. Français.