Utilisateur:Jean-Michel Tanguy/SujetENTPE2021/JUILLARD - MESSIAEN - SARRADE

Contexte

En raison du changement climatique, le niveau des mers et des océans ne cesse d’augmenter. Cette hausse provoque de nombreuses conséquences sur le territoire et les habitants. En effet, l’érosion des côtes augmentent, détruisant les infrastructures et entraînant le départ des habitants.

A travers ce projet, nous étudierons l'impact du réchauffement climatique sur le littoral et notamment l’impact de la houle sur le littoral. Nous utiliserons le modèle de Berkhoff afin de modéliser les houles.

Le modèle de Berkhoff

Nous utilisons le modèle de Berkhoff afin de modéliser la houle. Ce modèle a pour expression :$ \nabla(CC_{g}\nabla(Ф))+k^{2}CC_{g}Ф = 0 $.
Nous utiliserons les notations suivantes :
ϕ : le potentiel
k : le nombre d’onde fonction de la profondeur H et de la fréquence ω (T est la période)

On a la relation implicite : $ ω^{2}=gktanh(kH) $
C : la célérité de l’onde
$ C_{g} $ : la célérité de groupe des vagues

Cas n°1 :

Nous sommes dans un domaine monodimensionnel plat de longueur L avec les conditions aux limites suivantes : $ Φ(x=0)=1 $ (condition de Dirichlet) et sortie libre amont $ \frac{\partial^{1}Φ(x=L)}{\partial x}=ikΦ(x=L) $ (condition de Robin).

On simplifie le problème en se plaçant dans le domaine des ondes longues : $ C=C_{g} $

On obtient donc : $ \frac{\partial^{2} Ф}{\partial x^2}+k^{2}Ф=0 $.

Résolution analytique :

Nous avons une équation homogène à coefficient constant : $ \frac{\partial^{2} Ф}{\partial x^2}+k^{2}Ф=0 $.

L'équation caractéristique est de la forme suivante : $ ax^{2}+bx+c=0 $. On calcule $ \Delta=-4k^{2} $.

On a : $ Φ(x) = Ae^{-ikx}+Be^{ikx} $ et $ \frac{\partial^{1}Φ(x)}{\partial x}=-ikAe^{-ikx}+ikBe^{ikx} $ avec (A,B) des constantes réelles à déterminer grâce aux conditions aux limites.

Conditions aux limites :

• $ Φ(x=0)=A+B=1 $, on a donc $ B = 1-A $.
• $ \frac{\partial^{1}Φ(x=L)}{\partial x} = ik(-Ae^{-ikL}+ikBe^{ikL})=ik(-Ae^{-ikL}+Be^{ikL}) $.

On a donc :

• $ A = 0 $
• $ B = 1 $

On obtient donc $ Φ(x)=e^{ikx} $.

Au final : $ \color{red}Ф(x,t)=e^{i(kx-ωt)} $.

L'évolution de la hauteur de la houle au cours du temps correspond à l'équation suivante : $ \color{red}h(x,t)=Re(Ф(x,t))=cos(kx-ωt) $.

Résolution par la méthode d'homotopie

La relation d'homotopie est la suivante : $ (1−p)\frac{\partial^{2} Ф}{\partial x^{2}}+p(\frac{\partial^{2} Ф}{\partial x^{2}}+k^{2}Ф)=0 $

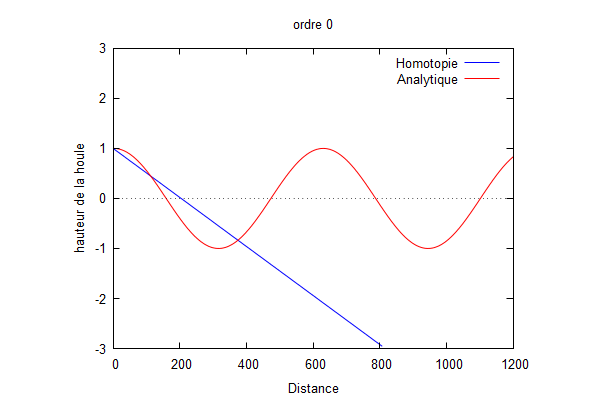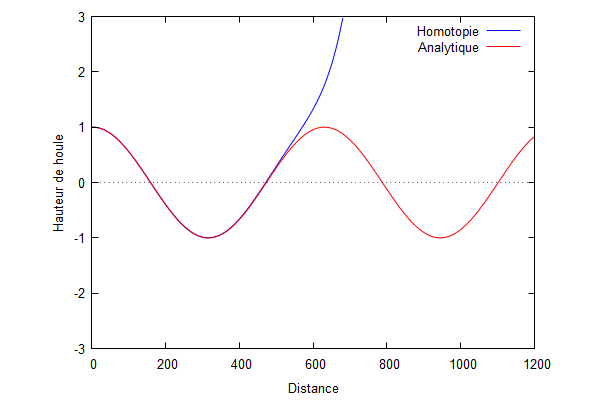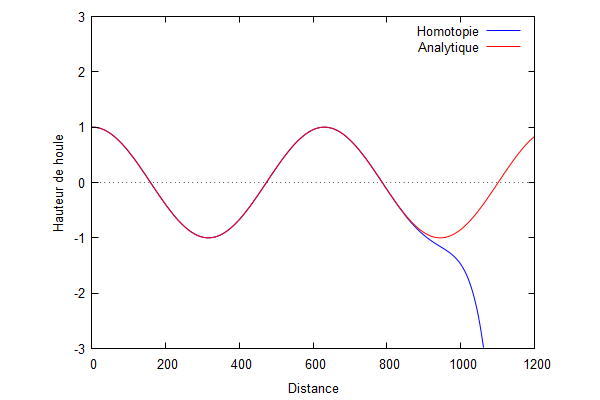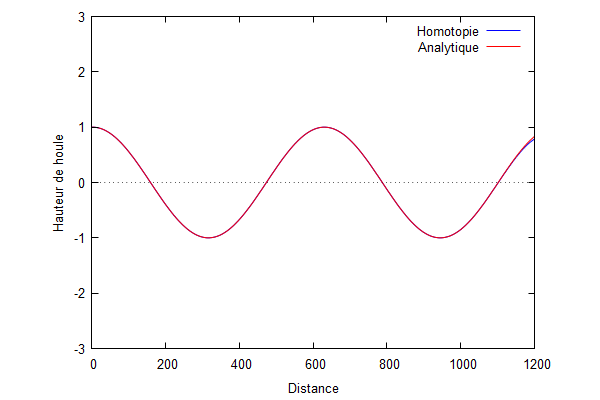
Ordre 0 :

On a : $ \frac{\partial^{2}Φ_{0}}{\partial x^{2}}=0 $

Donc $ Φ_{0}= Ax+B $ avec A et B deux constantes réelles à déterminer grâce aux conditions aux limites :

• $ Φ_{0}(x=0)=1 $ ↔ $ B=1 $
• $ Φ_{0}(x=L)=ikΦ_{0}(x=L) $ ↔ $ A=\frac{ik}{1-ikL} $

On a donc $ \color{red}Φ_{0}=\frac{ik}{1-ikL}x+1 $.

Ordre 1 :

On a : $ Ф_{1,xx}+k^{2}Ф_{0}=0 $ Donc : $ Ф_{1}=-k^{2}\iint(Ф_{0})+Ax+B $ avec A et B deux constantes réelles à déterminer grâce aux conditions aux limites :

• $ Ф_{1}(x=0)=0 $
• $ Ф_{1,x}(x=L)=ikФ_{1}(x=L) $.

On obtient donc : $ \color{red}Ф_{1}=-k^{2}\frac{ik}{6(1-ikL)}x^{3}+k^{2}\frac{1}{2}x^{2}-\frac{k^{2}L(k^{2}L^{2}+3ikL-3)}{3(1-ikL)^{2}}x $

Ordres supérieurs :

On utilise le logiciel wxmaxima afin de trouver Φ à tous les ordres.

Nous prenons : $ k=\frac{1}{100} $, $ L=\frac{1}{k} $

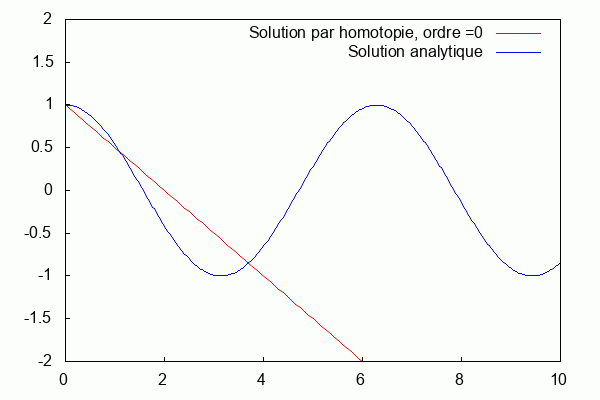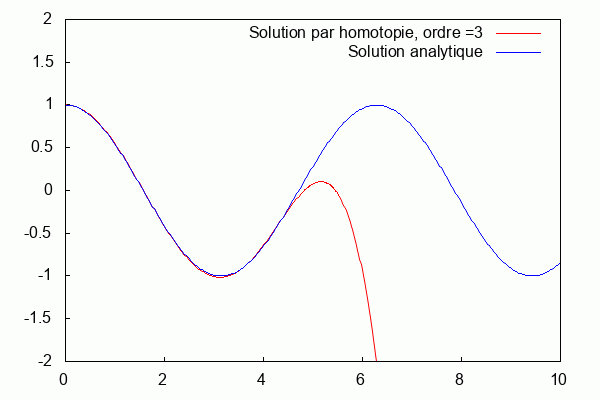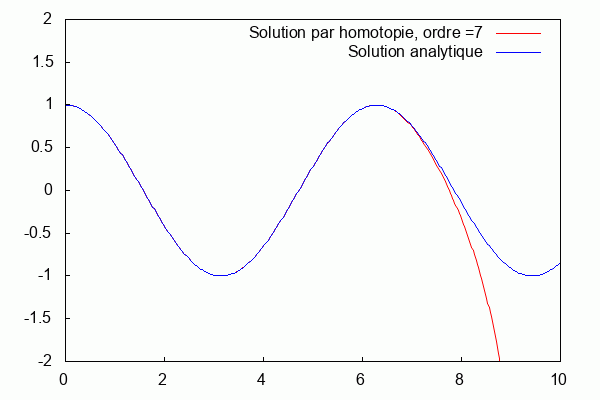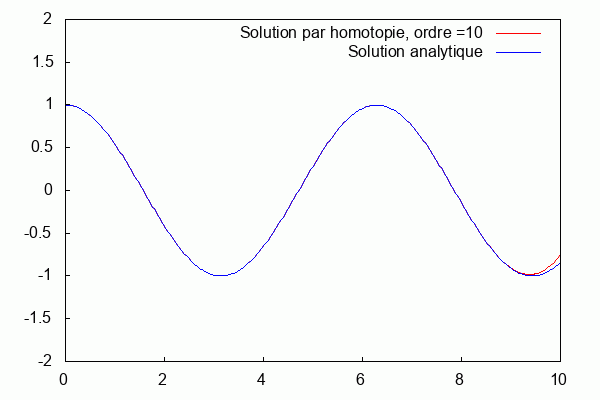
On superpose la solution analytique et la solution par homotopie.

Nous pouvons voir que la solution d'homotopie (courbe bleue) converge vers la solution analytique (courbe rouge) lorsque les ordres augmentent.

Etude de la sensibilité de la solution en fonction du nombre d'onde

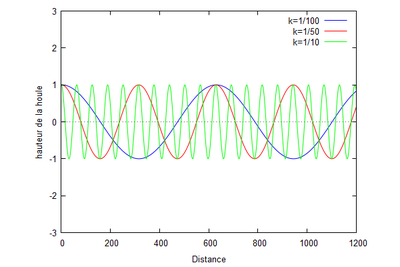
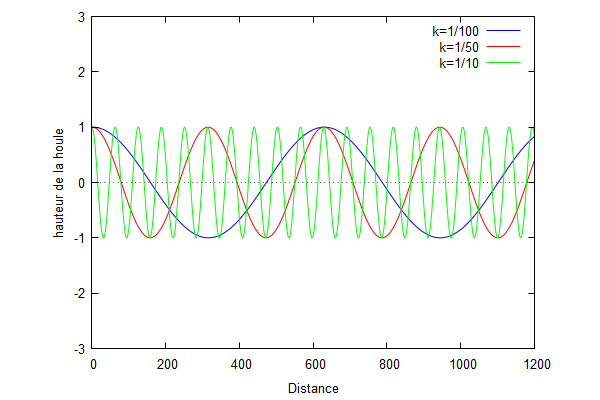
Nous traçons les courbes de l'équation de la hauteur de la houle en fonction de la distance en faisant varier le nombre d'onde. Nous obtenons la figure suivante :

Nous pouvons voir que lorsque le nombre d'onde augmente, la fréquence des vagues augmentent et donc la période diminuent. Par conséquent, les vagues sont plus nombreuses mais plus petites lorsque le nombre d'onde augmente. Ces vagues parcourent de faible distance en raison de la dissipation d'énergie. Inversement, pour un faible nombre d'onde, les vagues sont plus longues et moins nombreuses et parcourent donc des distances plus importantes. En revanche, nous pouvons voir que la hauteur de la houle n'est pas modifiée lorsque l'on modifie le nombre d'onde.

Réflexion portant sur l'analyse des résultats, les limites et l'intérêt de la méthode d'homotopie

La méthode d'homotopie permet de déterminer les solutions du modèle à partir de solutions simples. Grâce au logiciel WXMAXIMA, nous avons pu tracer l'évolution de la hauteur de la houle en fonction du temps.

Grâce à ce modèle, nous étudions un cas simple de modélisation de la houle. En effet, nous avons fait l'hypothèse d'une onde monodimensionnelle alors qu'en réalité il s'agit d'une onde tridimensionnelle. De plus, de nombreux paramètres ne sont pas pris en compte : irrégularité des fonds océaniques (les fonds marins dessinent le relief à la surface des océans) et des littoraux. Nous ne prenons pas en compte l'érosion des roches sur les côtes.

Cas n°2 :

Nous sommes dans le domaine monodimensionnel plat de longueur L avec les conditions aux limites suivantes : $ \frac{\partialΦ(x=0)}{\partial x}=ik(2-Φ(x=0)) $ en aval et $ \frac{\partialΦ(x=L)}{\partial x}=0 $ en amont.

Résolution analytique :

De la même manière que le cas n°1, le modèle de Berkhoff devient : $ \frac{\partial^{2} Ф}{\partial x^2}+k^{2}=0 $.

On obtient donc :

• $ \frac{\partialΦ(x=0)}{\partial x}=ik(-A+B)=ik(2-Φ(x=0))=ik(2-A-B) $ ↔ $ B=1 $
• $ \frac{\partialΦ(x=L)}{\partial x}=ik(-Ae^{-ikL}+Be^{ikL}=0 $ ↔ $ A=e^{2ikL} $.

On a donc : $ Φ(x)=e^{ik(2L-x)}+e^{ikx} $.

Au final : $ \color{red}Φ(x,t)=e^{i(-wt+k(2L-x))}+e^{kw-wt} $.

L'évolution de la hauteur de la houle au cours du temps correspond à l'équation suivante : $ \color{red}h(x,t)=Re(Ф(x,t))=cos(k(2L-x)-ωt)+cos(kx-wt) $.

Résolution par la méthode d'homotopie :

La relation d'homotopie est la suivante : $ (1−p)\frac{\partial^{2} Ф}{\partial x^2}+p(\frac{\partial^{2} Ф}{\partial x^2}+k^{2}Ф)=0 $. Mais dans ce cas n°2, les conditions aux limites sont différentes.

Ordre 0 :

On a $ Φ_{0,xx}=0 $ et donc $ Φ_{0}=Ax+B $.

Conditions aux limites :

• $ \frac{\partialΦ_{0,x}(x=L)}{\partial x}=0=A $.
• $ \frac{\partialΦ_{0,x}(x=0)}{\partial x}=ik(2-Φ(x=0))=ik(2-B)↔B=2 $.

On obtient ainsi : $ \color{red}Φ_{0}(x)=2 $.

Ordre 1 :

On a $ Φ_{1,xx}+k^{2}Φ_{0}=0 $ et donc $ Φ_{1}=-2k^{2}x^{2}+Ax+B $

Conditions aux limites :

• $ A=2k^{2}L $
• $ B=\frac{A}{-ik} $

On obtient ainsi : $ \color{red}Φ_{1}(x)=-k^{2}x^{2}+2k^{2}Lx+2ikL $.

Ordres supérieurs :

On utilise le logiciel wxmaxima afin de trouver Φ à tous les ordres.

On superpose la solution analytique et la solution par homotopie.

Nous prenons : $ k=\frac{1}{100} $, $ L=20 $

Nous pouvons voir que la solution d'homotopie (courbe bleue) converge vers la solution analytique (courbe rouge) lorsque les ordres augmentent.

Etude de la sensibilité de la solution en fonction du nombre d'onde

Comme pour le cas 1, nous traçons les courbes de l'équation de la hauteur de la houle en fonction de la distance en faisant varier le nombre d'onde.

De la même manière que le cas 1, nous retrouvons la même évolution de la fréquence de la houle : lorsque le nombre d'onde augmente, la fréquence des vagues augmentent et donc la période diminuent. Contrairement au cas 1, nous pouvons voir que la hauteur de la houle est modifiée lorsque l'on modifie le nombre d'onde.

Réflexion portant sur l'analyse des résultats, les limites et l'intérêt de la méthode d'homotopie

Comme pour le cas 1, la méthode d'homotopie ne permet de pas prendre en compte tous les paramètres qui modélisent la houle (onde tridimensionnelle, érosion des roches,...)

Cas n°3

Nous sommes dans le domaine monodimensionnel plat de longueur L avec la pente du fond constante (s=cste) les conditions aux limites sont les suivantes $ Φ(x=0)=1 $ en aval et $ \frac{\partial^{1}Φ(x=L)}{\partial x})=ikΦ(x=L) $ en amont.

Le modèle de Berkhoff devient : $ H(x)Φ_{xx}-H'(x)Φ_{x}+k^{2}H(x)Φ=0 $ avec $ H(x)=H0-sx $ avec $ H(x)=H_{0}-sx $ et $ k=k0=constante $.

Résolution analytique

On effectue un changement de variable $ z=H0-sx $

Résolution par la méthode d′homotopie:

On a la relation d'homotopie suivante : $ (1-p)Φ_{xx}+p((H0-sx)Φ_{xx}-Φ_xx)-sΦ_{x}+k^2((H0-sx)Φ_{x})=0 $

Ordre 0

On a : $ \frac{\partial^{2}Φ_{0}}{\partial x^{2}}=0 $

On a donc : $ Φ_{0}= Ax+B $

Avec les conditions initiales, on obtient : $ \color{red}Φ_{0}=\frac{ik}{1-ikL}x+1 $.

Ordre 1

On a : $ Φ_{1,xx}-Φ_{0,xx}+(1-ε)Φ_{0,xx}-εΦ_{0,x}+k^{2}Φ_{0}=0 $ avec $ ε=\frac{s}{H_{0}} $.

On obtient donc : $ Φ_{1,xx}=εΦ_{0,xx}+εΦ_{0,x}-k^{2}Φ_{0} $

Donc $ Φ_{1}=\iint(εΦ_{0,x}-k^{2}Φ_{0})+Ax+B $.

Avec les conditions aux limites, on obtient :

Cas n°4

Nous sommes dans un canal monodimensionnel de largeur uniforme, de longueur L avec la forme du fond exponentielle. Les conditions aux limites sont les suivantes $ Φ(x=0)=1 $ en aval et $ \frac{\partial^{1}Φ(x=L)}{\partial x})=ikΦ(x=L) $ en amont.

Dans ce cas n°4, $ H(x)=H0e^{-sx} $ et l'équation de Berkhoff devient : $ Φ_{xx}-sΦ(x)+k^{2}Φ(x)=0 $

On calcule le discriminant : $ Δ=s^{2}-4k^{2} $

• Si $ Δ>0 $ :

On a deux racines réelles : $ x_{1}=\frac{s-sqrt{s^{2}-4k^{2}}}{2} $ et $ x_{2}=\frac{s+sqrt{s^{2}-4k^{2}}}{2} $

On a donc : $ Φ(x)=Ae^{\frac{(s-sqrt{s^{2}-4k^{2}})x}{2}}+Be^{\frac{(s+sqrt{s^{2}-4k^{2})x}}{2}} $.

Avec les conditions aux limites, on obtient :

• Si $ Δ=0 $ :

On a $ x_{0}=\frac{s}{2} $

On a donc : $ Φ(x)=(Ax+B)e^{\frac{sx}{2}} $

• Si $ Δ<0 $ :

On a $ x_{1}=\frac{s-isqrt{s^{2}-4k^{2}}}{2} $ et $ x_{2}=\frac{s+isqrt{s^{2}-4k^{2}}}{2} $

On a donc : $ Φ(x)=e^{\frac{sx}{2}}(Acos(sqrt{\frac{s^{2}-4k^{2}}{2}}}x)+Bsin(sqrt{\frac{s^{2}-4k^{2}}{2}}}x)) $